About this post

In the last post, I introduced the ADS1220 24-bit, 4-channel A/D converter and my associated library. In this sequel, I will show you how to use the ADS1220 to take advantage of its benefits with practical examples.

I use the examples in the data sheet as a guide. To focus on the essentials, I have simplified the circuits. Most importantly, I left out all the RC filters, which can be a bit confusing for beginners. Even without them, I have achieved excellent results. However, if you want to reduce noise and interference even further, it’s worth taking a look at the data sheet.

Let’s take a look at the following applications:

• Thermocouples (type K)
• Resistance thermometers
  • NTCs (thermistors)
  • RTDs (PTC thermistors)
    
    • PT1000, 2-wire circuit
      • Direct measurement
      • Measurement using reference resistors
    • PT100
      • 3-wire circuit
      • 4-wire circuit
• Wheatstone bridges

Controlling thermocouples (type K) with the ADS1220

How does a thermocouple work?

In a nutshell: Thermocouples consist of two wires made from different metals connected at one of their ends. If there is a temperature difference along the wires, you can measure a voltage between the free ends. This is the Seebeck effect. Different metal pairings have different temperature-voltage characteristics. However, they have in common that they are almost linear over a wide range. Basically, the effect, i.e. the voltage change per degree, is small.

You can find temperature-voltage tables for the different thermocouples in many places on the net. The reference temperature is always 0° C. A disadvantage of thermocouples is that you can only measure temperature differences. The temperature at the point where you measure the voltage must be known.

Very widespread is the type K, which consists of the pairing nickel/nickel-chromium. With it, the voltage change is about 40 microvolts per degree, or about 4 millivolts per 100 °C. That’s not really much. And that’s why we need a high-resolution, low-noise, high-gain ADC here. This is an ideal challenge for the ADS1220.

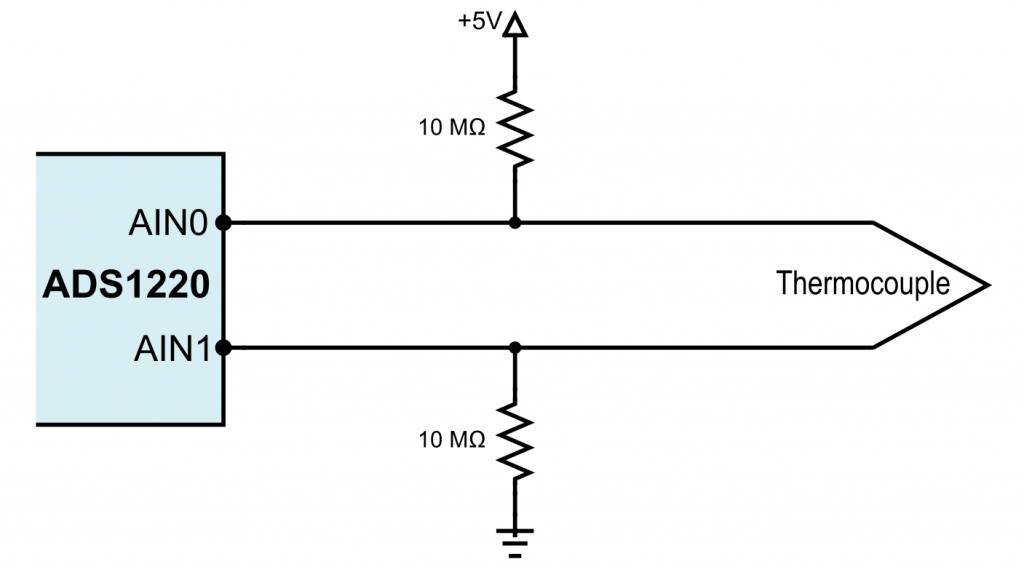
The circuit on the ADS1220

We remember (and if not, check the last post): For the reliable operation of the PGA, i.e. the amplifier of the ADS1220, the output voltage of the PGA must be at least 200 millivolts above AVSS and at most 200 millivolts below AVDD. So, you must not perform “single-ended” measurements against AVSS. At least not if you want to apply a gain greater than 4.

Ideally, you work with input voltages that are close to (AVSS+AVDD)/2. You can achieve this with the following circuit:

The two 10 megohm resistors force the voltage to be in the middle range. Their size prevents larger currents from flowing across the thermocouple and distorting the result. The ADS1220 data sheet recommends resistor values between 1 and 50 megohms.

The voltage of 5 volts is chosen arbitrarily. You can also, for example, apply 3.3 volts. And instead of the AIN0 and AIN1 inputs, the other inputs would be equally suitable.

Here is the complete circuit as a Fritzing scheme:

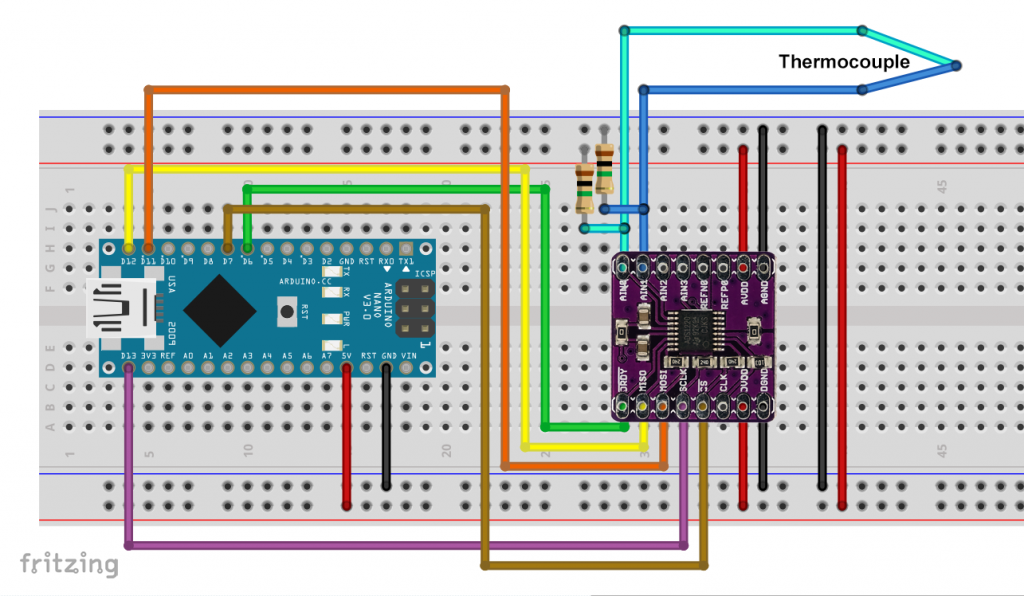
Do you notice that there are 1 megohm resistors shown here? The simple reason is that I have not found any 10 megohm resistors at Fritzing! However, 10 megohm resistors were actually used.

Regression lines and polynomials for the characteristic curves

In the following, we will measure thermoelectric voltages and calculate the temperature from them. For this purpose, I copied the thermoelectric voltage / temperature values for the thermocouple K into Excel and calculated regression functions (trendlines) from them. I limited myself to the range between -20 and +110 °C. The regression curves are only valid for this area.

As you can see, the linear approach is not bad for this relatively small temperature range. However, the square function on the right fits even better. If you want to cover larger temperature ranges, you should at least work with a quadratic function. I’m trying both here.

Linear approach

The linear approach is simple. You measure the ambient temperature with the internal thermometer of the ADS1220 or another temperature sensor. From the measured voltage, the sketch calculates the temperature difference and adds it to the ambient temperature.

Since the expected voltages are only a few millivolts, we can safely apply a gain of 128 and use the internal voltage reference (+/- 2.048 volts).

#include <ADS1220_WE.h>
#include <SPI.h>

#define ADS1220_CS_PIN    7 // chip select pin
#define ADS1220_DRDY_PIN  6 // data ready pin 

ADS1220_WE ads = ADS1220_WE(ADS1220_CS_PIN, ADS1220_DRDY_PIN);

void setup(){
  Serial.begin(9600);
  if(!ads.init()){
    Serial.println("ADS1220 is not connected!");
    while(1);
  }
  ads.setCompareChannels(ADS1220_MUX_0_1);
  ads.setGain(ADS1220_GAIN_128);
}

void loop(){
  float ambTemp = 0.0;
  float deltaTemp = 0.0; // thermocouple temperature minus ambient temperature
  float tCTemp = 0.0; // thermocouple temperature
  float tCV = 0.0; // thermocouple voltage
  
  ads.enableTemperatureSensor(true);
  ambTemp = ads.getTemperature();
  ads.enableTemperatureSensor(false); 
  Serial.print("Ambient Temperature [°C]:          ");
  Serial.println(ambTemp);

  tCV = ads.getVoltage_muV(); // get result in millivolts
  deltaTemp = 0.0244821*tCV + 0.106873;
  Serial.print("Thermocouple T vs. ambient T [°C]: ");
  Serial.println(deltaTemp);
  
  tCTemp = ambTemp + deltaTemp;
  Serial.print("Thermocouple Temperature [°C]:     ");
  Serial.println(tCTemp);
  Serial.println();

  delay(2000);
}

For the following output, I put the thermocouple in a cup of warm water. You can see nicely how the water cools down. A reference thermometer with a guaranteed maximum deviation of 0.2 °C was used for verification. The values determined with the thermocouple deviated from this by only a few tenths of a degree.

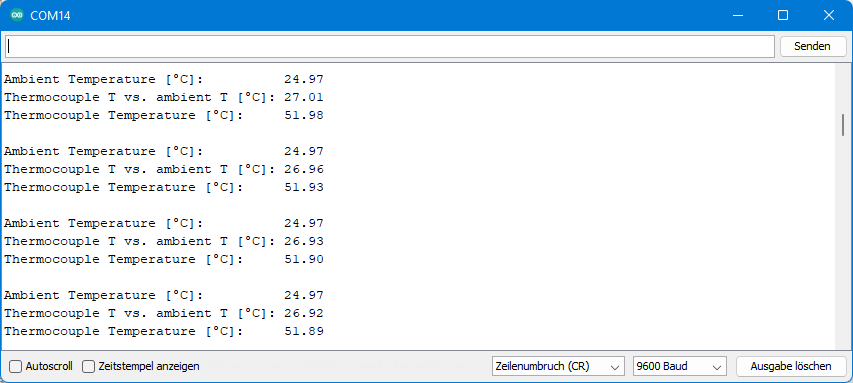
Polynomial approach

With the polynomial method, things are a little more complicated because we have to consider that the characteristic curve is referred to 0 °C. We measure the ambient temperature again with the ADS1220, but first calculate the thermoelectric voltage referred to 0 °C from it. To do this, we need another polynomial regression curve with the axes reversed (x = temperature, y = thermoelectric voltage). I’m not showing these curves here. We add this calculated voltage (voltage correction “vC”) to the measured thermoelectric voltage and insert the result into the polynomial regression curve.

This is the sketch:

#include <ADS1220_WE.h>
#include <SPI.h>

#define ADS1220_CS_PIN    7 // chip select pin
#define ADS1220_DRDY_PIN  6 // data ready pin 

ADS1220_WE ads = ADS1220_WE(ADS1220_CS_PIN, ADS1220_DRDY_PIN);

void setup(){
  Serial.begin(9600);
  if(!ads.init()){
    Serial.println("ADS1220 is not connected!");
    while(1);
  }
  ads.setCompareChannels(ADS1220_MUX_0_1);
  ads.setGain(ADS1220_GAIN_128);
}

void loop(){
  float ambTemp = 0.0;
  float tCTemp = 0.0; // thermocouple temperature
  float tCV = 0.0; // thermocouple voltage
  float vC = 0.0; // voltage correction (deviation from 0°C)

  ads.enableTemperatureSensor(true);
  ambTemp = ads.getTemperature();
  ads.enableTemperatureSensor(false); 
  Serial.print("Ambient Temperature [°C]:        ");
  Serial.println(ambTemp);
  
  vC = 1.16946*pow(ambTemp,2)*pow(10,-2) + 39.8013*ambTemp + 2.5078; 
  Serial.print("Voltage Compensation [µV]:       ");
  Serial.println(vC);

  tCV = ads.getVoltage_muV(); // get result in millivolts
  Serial.print("Thermocouple Voltage [µV]:       ");
  Serial.println(tCV);
  tCV += vC;
  Serial.print("Corr. Thermocouple Voltage [µV]: ");
  Serial.println(tCV);

  tCTemp = -1.71627*pow(tCV,2)*pow(10,-7) + 2.51112*pow(10,-2)*tCV - 0.0664632;
  Serial.print("Thermocouple Temperature [°C]:   ");
  Serial.println(tCTemp);
  Serial.println();

  delay(2000);
}

And this is what the output looked like on my end:

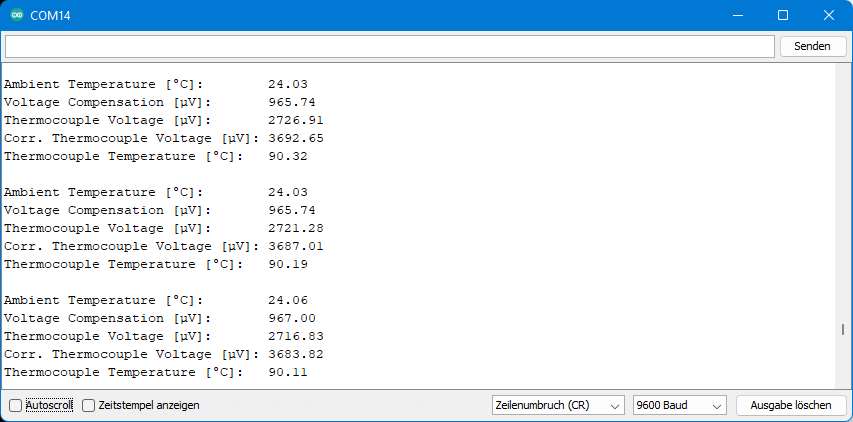
Again, a cup of hot water was used for this test.

Resistance thermometers

Unlike thermocouples, which provide a temperature-dependent voltage, resistance thermometers change their resistance with temperature. Their advantage is that you can determine the temperatures absolutely, i.e. without reference temperature.

The family of resistance thermometers consists of NTCs and the RTDs. NTC stands for “Negative Temperature Coefficient Thermistor”. That is, the resistance decreases with temperature. In German, NTCs are also referred to as hot conductors (“Heißleiter”). NTCs are characterized by comparatively high resistance values because they are made of metal oxides.

RTD stands for “Resistance Temperature Detector”. In this respect, one would assume that an NTC is also an RTD. However, only those thermometers whose resistance decreases with increasing temperature are called RTDs. These include the well-known “PT100” and “PT1000”.  They are also referred to as PTCs or PTC thermistors. The number stands for the resistance at 0 °C, and the “PT” for the material used, namely platinum.

According to Ohm’s law, the resistance can be determined by a known current, and this can be provided by the ADS1220. Alternatively, you can also use a reference resistor which you connect in series with the resistance thermometer. But one by one.

Controlling NTCs (thermistors) with the ADS1220

Characteristic curve of the NTC

NTCs are classified according to their resistance value at 25 °C. For this article, I have chosen a 10 kiloohm model. Ideally, the manufacturers specify the so-called B-value, with which you can calculate the resistance R at a given temperature T compared to the reference temperature T_ref:

R_{\text{T}}=R_{\text{T{ref}}}\cdot \text{e}^{B\cdot\left( \frac{1}{\text{T}}-\frac{1}{\text{T{ref}}}\right)} 

My 10 kΩ NTC did not have a B value specified, but it did have a table of values. I have tried various regression functions in Excel. For a satisfactory result, I had to divide the range of values into three parts. There are certainly better math programs that have more appropriate functions implemented. But Excel is accessible to almost everyone.

Measurement with the ADS1220

First of all, the method described here is not the most accurate. However, a few trial measurements showed deviations well below one degree. Besides, the method is simple. An error analysis still follows. It is better to use reference resistors. I will show this with the example of PTCs.

To measure the temperature dependent resistance, we use the IDAC function of the ADS1220. The measuring range I have chosen starts at 0 °C. At this temperature, the resistance is 32.69 kiloohm. At a current of 50 microamps, this results in a voltage of ~1.63 volts. This can still be measured well with the internal reference of the ADS1220, and the value is still well below the limit of AVDD – 0.9 volts. We must choose 1 as the gain factor.

The lowest resistance is ~0.5 kiloohm. With an IDAC of 50 microamperes, the voltage at the NTC is 25 millivolts. Since the gain factor is 1, this would also be the lower limit for the output voltage of the PGA. This is below the limit of AVSS + 200 millivolts. That’s why we need to bypass the PGA.

I used the following simple setup:

The sketch for this is also simple:

#include <ADS1220_WE.h>
#include <SPI.h>

#define ADS1220_CS_PIN    7 // chip select pin
#define ADS1220_DRDY_PIN  6 // data ready pin 

ADS1220_WE ads = ADS1220_WE(ADS1220_CS_PIN, ADS1220_DRDY_PIN);

void setup(){
  Serial.begin(9600);
  if(!ads.init()){
    Serial.println("ADS1220 is not connected!");
    while(1);
  }

  ads.setCompareChannels(ADS1220_MUX_0_3);
  ads.setGain(ADS1220_GAIN_1);
  ads.bypassPGA(true); // true disables PGA, false enables PGA
  ads.setIdacCurrent(ADS1220_IDAC_50_MU_A);
  ads.setIdac1Routing(ADS1220_IDAC_AIN0_REFP1);
} 

void loop(){
  float result = 0.0;
  float resistanceInKiloOhm = 0.0;
  float temperature = 0.0;

  result = ads.getVoltage_mV(); // get result in millivolts
  Serial.print("Voltage [mV]:      ");
  Serial.println(result,3);
  
  resistanceInKiloOhm = result / 50.0;
  Serial.print("Resistance [kOhm]: ");
  Serial.println(resistanceInKiloOhm,3);
  
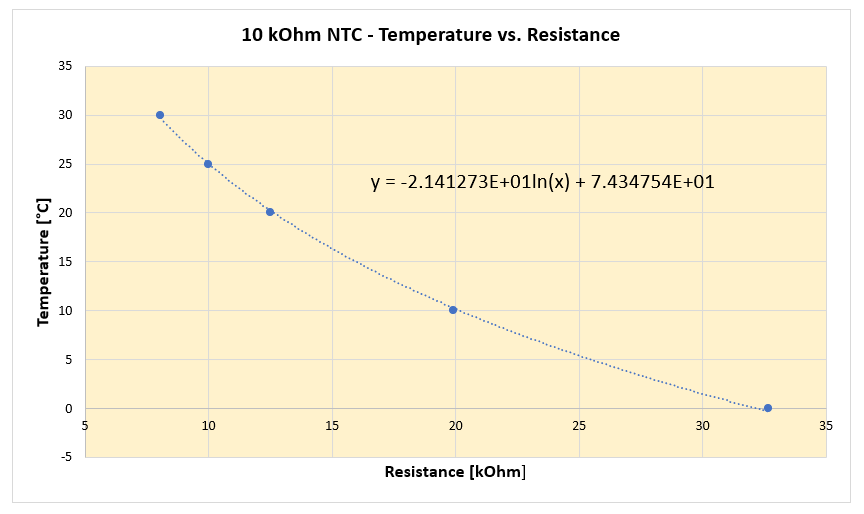
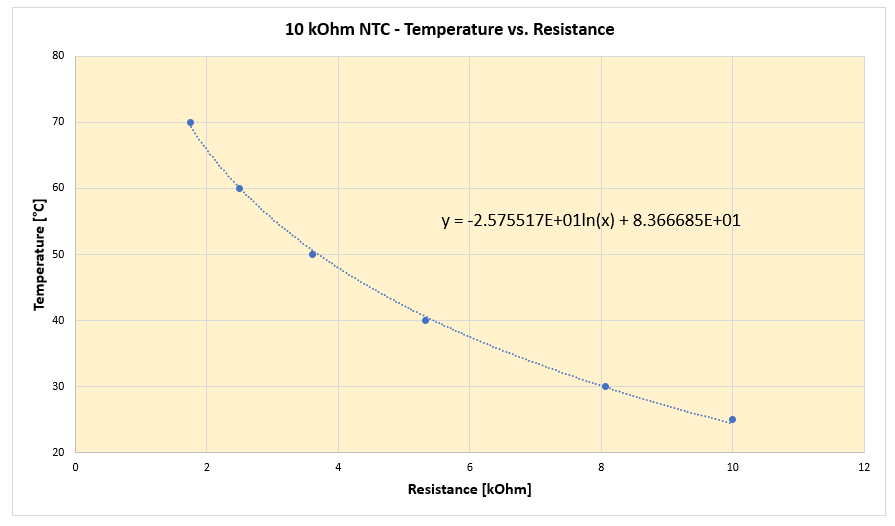
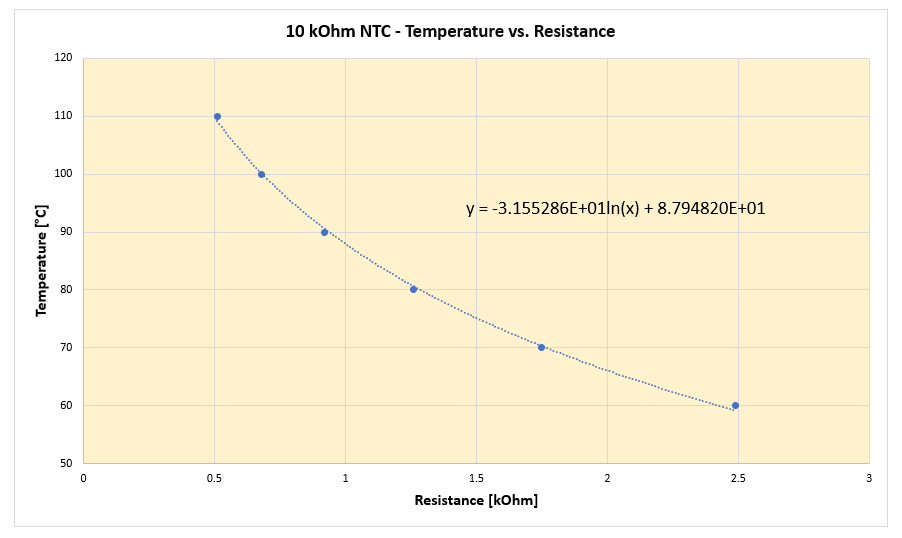
  if(resistanceInKiloOhm > 9.0){
    temperature = -21.41273 * log(resistanceInKiloOhm) + 74.34754;
  }
  else if(resistanceInKiloOhm > 2.2){
    temperature = -25.75517 * log(resistanceInKiloOhm) + 83.366685;
  }
  else{
    temperature = -31.55286 * log(resistanceInKiloOhm) + 87.9482;
  }
  Serial.print("Temperature [°C]:  ");
  Serial.println(temperature);
  
  Serial.println();
  delay(2000);
}

And this is what the output looked like:

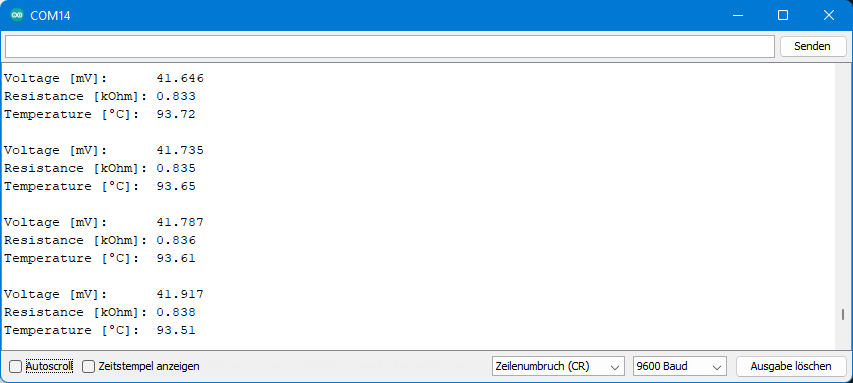
Error analysis

The data sheet specifies a typical deviation of +/- 1% for the IDAC. This error has a proportional effect on the determined resistance value. At 25 °C the resistance is 10 kΩ. What if we were to determine only 9.9 kΩ? When used in the regression function, this would result in a temperature of ~25.26 °C. The error is smaller than some might have thought. This is where the non-linear shape of the characteristic curve is beneficial.

However, the data sheet specifies +/- 6% as the maximum deviation of the IDAC. At 9.4 kΩ the temperature would be 26.37 °C. However, I am unable to say how likely it is that these maximum deviations of the IDAC actually occur.

The error of the reference voltage also has a directly proportional effect on the result. The data sheet specifies arange of 2,045 – 2,051 volts. This corresponds to about +/- 0.15%, so it is a rather small error.

In addition, there is an error caused by the lead resistance. At 25 °C (= 10 kΩ NTC resistance) this does not matter much. At 150 °C, however, the resistance is only 180 ohms according to the manufacturer’s table. Therefore, a long lead could influence the result.

Controlling RTDs (PTC thermistors) with the ADS1220

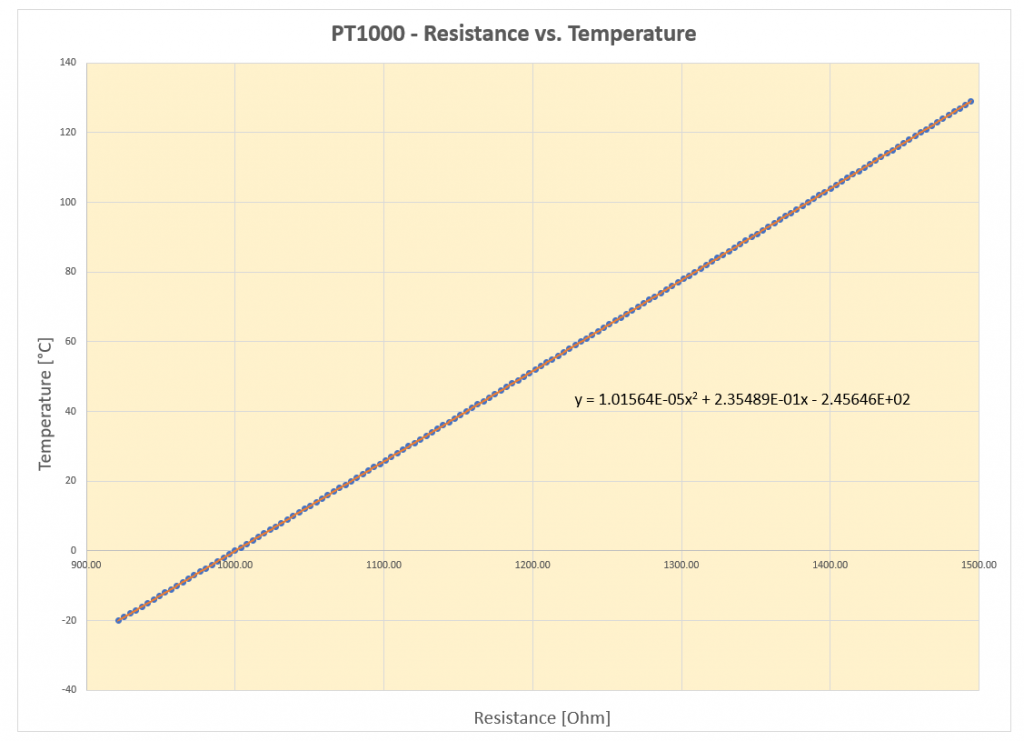
PT1000

The PT1000 has an almost linear characteristic curve. However, to match the resistance/temperature values even better, I chose a quadratic compensation curve:

Direct measurement with the ADS1220

First, I proceeded as I did with the NTC. This is not really recommended for PT1000, but I want to show the difference.

For the temperature range I considered, the resistance of the PT100 is ~1.5 kΩ maximum. That is why we can choose a higher IDAC current and gain in this case. However, the PGA must still be bypassed. With an IDAC of 250 µA, a gain of 4 and a maximum resistance of 1.5 kΩ, the maximum voltage (after amplification) is 1.5 volts, so the internal reference can be used.

#include <ADS1220_WE.h>
#include <SPI.h>

#define ADS1220_CS_PIN    7 // chip select pin
#define ADS1220_DRDY_PIN  6 // data ready pin 

ADS1220_WE ads = ADS1220_WE(ADS1220_CS_PIN, ADS1220_DRDY_PIN);

void setup(){
  Serial.begin(9600);
  if(!ads.init()){
    Serial.println("ADS1220 is not connected!");
    while(1);
  }

  ads.setCompareChannels(ADS1220_MUX_0_3);
  ads.setGain(ADS1220_GAIN_4);
  ads.bypassPGA(true); // true disables PGA, false enables PGA
  ads.setIdacCurrent(ADS1220_IDAC_250_MU_A);
  ads.setIdac1Routing(ADS1220_IDAC_AIN0_REFP1);
} 

void loop(){
  float result = 0.0;
  float resistanceInOhm = 0.0;
  float temperature = 0.0;
  float ambTemp = 0.0;

  ads.enableTemperatureSensor(true);
  ambTemp = ads.getTemperature();
  ads.enableTemperatureSensor(false); 
  Serial.print("Ambient Temperature [°C]: ");
  Serial.println(ambTemp);
  
  result = ads.getVoltage_mV(); // get result in millivolts
  Serial.print("Voltage [mV]:             ");
  Serial.println(result,3);
  
  resistanceInOhm = result / 0.25;
  Serial.print("Resistance [kOhm]:        ");
  Serial.println(resistanceInOhm);

  temperature = 1.01564*pow(10,-5)*pow(resistanceInOhm,2) + 0.235489*resistanceInOhm - 245.646;
  Serial.print("Temperature [°C]:         ");
  Serial.println(temperature);
  
  Serial.println();
  delay(2000);
}

And here is the output. I measured against the internal temperature sensor of the ADS1220 for comparison.

Error analysis

Due to the almost linear shape of the characteristic curve, errors in the IDAC are much more noticeable than in the NTC. A deviation of only one percent results in a deviation of 2.6 °C. With this in mind, my readings above are already pretty good.

Measurement with the ADS1220 via a reference resistor

To eliminate the dependence on deviations of the IDAC, we let the current flow through a reference resistor after passing through the RTD and take this voltage as the reference voltage:

According to Ohm’s law

\frac{U_{\text{RTD}}}{R_{\text{RTD}}} = I_{\text{IDAC1}} = \frac{U_{\text{RRef}}}{R_{\text{RRef}}}

\Longrightarrow\;\;\;\; R_{\text{RTD}}=R_{\text{RRef}}\cdot \frac{U_{\text{RTD}}}{U_{\text{RRef}}}

The reference voltage must be at least as large as the voltage to be measured. This means that the reference resistance must be at least as large as the largest resistance of RTD. I designed my circuit for RTD values up to 1.5 kΩ and chose an appropriate resistor. A measurement with my multimeter showed a value of 1.483 kΩ.

With an IDAC of 1 mA and a total resistance of ~3 kΩ, the maximum voltage at AIN1 is 3 volts. If you use a supply voltage (AVDD) of 5 volts, that is far below the limit of AVDD minus 0.9 volts. If you use lower supply voltages, like 3.3 volts, then you have to reduce the IDAC accordingly.

In the following sketch, REFP0/REFN0 is set as the equivalent voltage. The exact value we specify for the equivalent voltage does not matter. The determined voltage at the RTD is proportional to this setting. And since we are dividing the voltages to determine R_RTD according to the equations above, the factor is truncated away. If this confuses you, you can alternatively work with the raw data (getRawData()) instead of the voltages.

The PGA does not need to be bypassed, since we are not getting close to the lower limit of AVSS plus 0.2 volts.

#include <ADS1220_WE.h>
#include <SPI.h>

#define ADS1220_CS_PIN    7 // chip select pin
#define ADS1220_DRDY_PIN  6 // data ready pin
#define VREF 2.0 // Reference Voltage, value does not matter

ADS1220_WE ads = ADS1220_WE(ADS1220_CS_PIN, ADS1220_DRDY_PIN);

void setup(){
  Serial.begin(9600);
  if(!ads.init()){
    Serial.println("ADS1220 is not connected!");
    while(1);
  }

  ads.setCompareChannels(ADS1220_MUX_1_0);
  ads.setGain(ADS1220_GAIN_1);
  ads.setVRefSource(ADS1220_VREF_REFP0_REFN0);
  ads.setVRefValue_V(VREF);  // exact value doesn't matter!
  ads.setIdacCurrent(ADS1220_IDAC_1000_MU_A);
  ads.setIdac1Routing(ADS1220_IDAC_AIN1);
} // end of setup()

void loop(){
  float result = 0.0;
  float resistanceInOhm = 0.0; 
  float temperature = 0.0;
  float ambTemp = 0.0;
  
  ads.enableTemperatureSensor(true);
  ambTemp = ads.getTemperature();
  ads.enableTemperatureSensor(false); 
  Serial.print("Ambient Temperature [°C]: ");
  Serial.println(ambTemp);

  ads.setCompareChannels(ADS1220_MUX_REFPX_REFNX_4);
  result = ads.getVoltage_mV();
  Serial.print("Reference Voltage [mV]:   ");
  Serial.println(result * 4.0);
  
  ads.setCompareChannels(ADS1220_MUX_1_0);
  result = ads.getVoltage_mV(); // get result in millivolts
  resistanceInOhm = result * 1.483 / VREF;
  Serial.print("Resistance [Ohm]:         ");
  Serial.println(resistanceInOhm);
  temperature = 1.01564*pow(10,-5)*pow(resistanceInOhm,2) + 0.235489*resistanceInOhm - 245.646;
  Serial.print("Temperature [°C]:         ");
  Serial.println(temperature);
  
  Serial.println();
  delay(2000);
}

And this is what my output looked like:

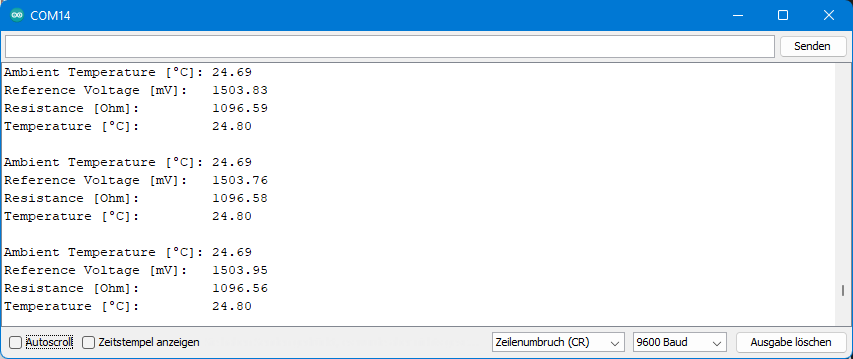
The temperatures determined with the PT1000 are in excellent match with those of the internal thermometer (“Ambient Temperature”). And both, in turn, did not deviate by more than two or three tenths of a degree from my high-precision reference thermometer in various measurements.

By the way, the output of the reference voltage is only used to check if things work as calculated. The value is not used any further. Theoretically, the reference voltage should be 1.483 volts. Perhaps the typical 1% deviation of IDAC comes into play here. Furthermore, according to the data sheet, the measurement of the external reference is not a precision measurement.

PT100

The measuring principle: 3-wire and 4-wire

The resistance of the PT100 at 0 °C is only 100 Ohm. As a result of this, another error comes into play here, namely the lead resistance R_LEAD. To compensate for the error, there are 3-wire or 4-wire PT100 (and PT1000!). In the case of the 3-wire PT100, one supply lead is doubled. With the 4-wire PT100, on the other hand, both lines are doubled. The double leads are each short-circuited before the sensor. Suitable circuits can be used to compensate for the lead influence.

3-wire circuit

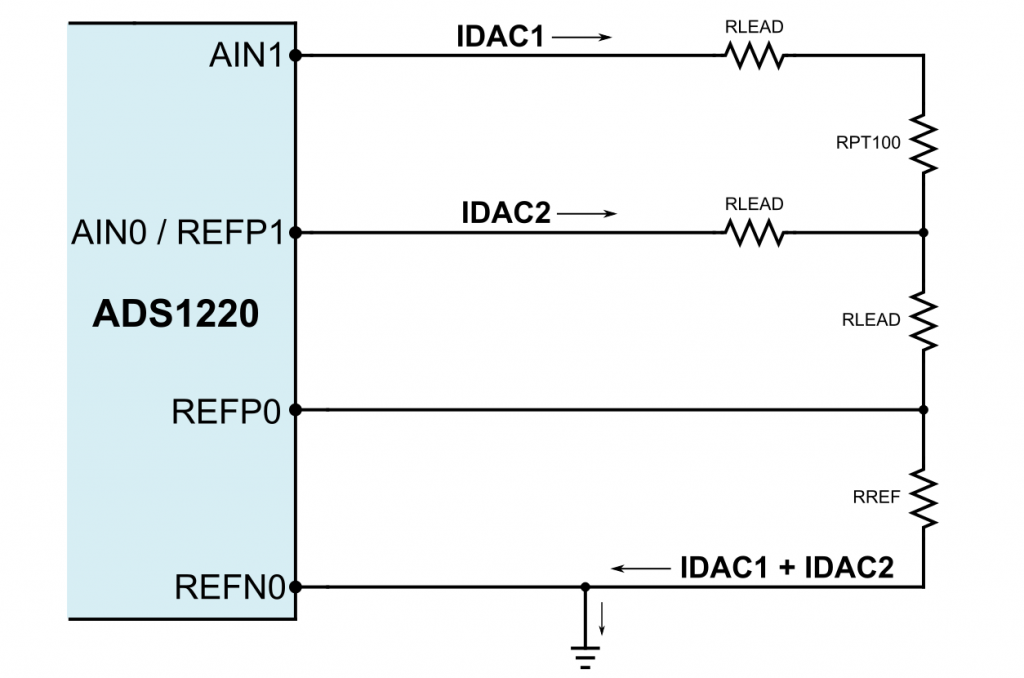
The following circuit can be applied to the 3-wire PT100:

To calculate the voltages AIN1 and AIN0, we just need to multiply the currents by the sum of the resistors through which they flow. The voltage difference between AIN1 and AIN0 is:

U_{\text{AIN1-AIN0}} = I_{\text{IDAC1}}\cdot \left(2\cdot R_{\text{LEAD}}  +R_{\text{PT100}} + R_{\text{REF}} \right) - I_{\text{IDAC2}}\cdot \left(2\cdot R_{\text{LEAD}}  + R_{\text{REF}} \right)

Since IDAC1 is equal to IDAC2, and we assume that the lead resistance values are all equal, after eliminating the brackets:

U_{\text{AIN1-AIN0}} = I_{\text{IDAC}}\cdot R_{\text{PT100}}  

This eliminates the resistance of the leads.

For the reference voltage applies:

U_{\text{REF}} = 2\cdot I_{\text{IDAC}}\cdot R_{\text{REF}}

If you divide the last two equations by each other and solve for RPT100, you get the following simple formula:

R_{\text{PT100}}  = 2\cdot\frac{U_{\text{AIN1-AIN0}}}{U_{\text{REF}}}\cdot R_{\text{REF}}

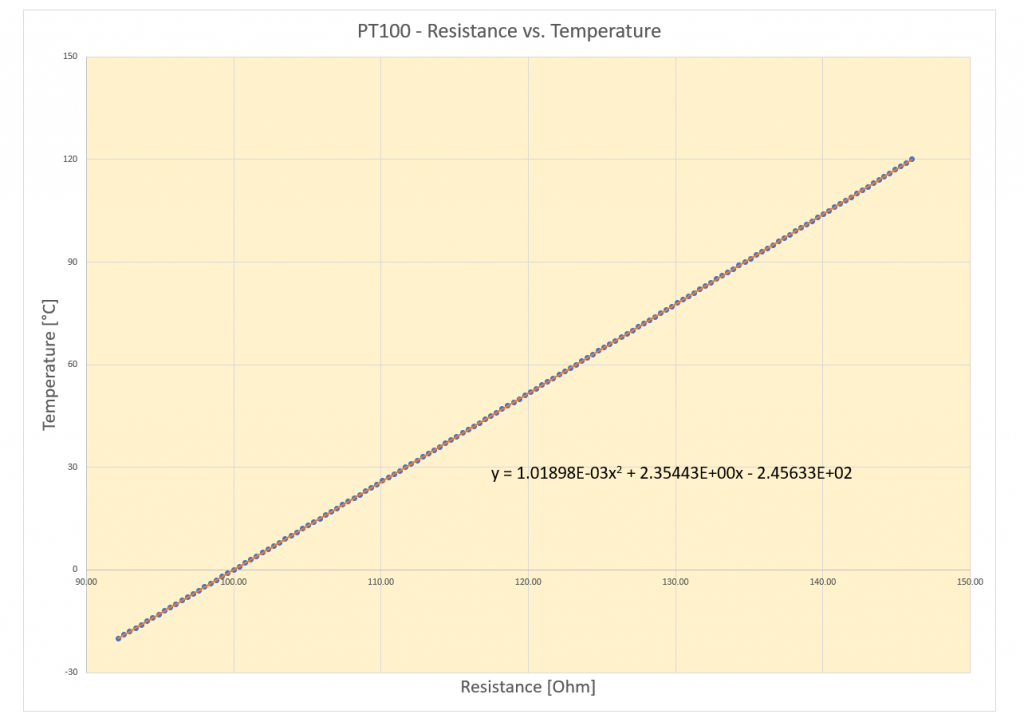
R_REF is known, we can measure the voltages, and a balancing polynomial was again used to convert R_PT100 to temperature:

As reference, I have chosen a 2.4 kΩ resistor (exactly: 2.403 kΩ). IDAC1 and IDAC2 were 500 microamperes each. Thus, the reference voltage is about 2.4 volts. In the temperature range I considered, the PT100 resistance is greater than 90 Ω and less than 150 Ω. U_AIN1-AIN0 is thus between 90 Ω x 500 µA and 150 Ω x 500 µA, i.e. between 45 mV and 75 mV. With a gain factor of 32, the limits of the PGA output voltage are thus 1.44 V and 2.4 V. All good!

Sketch and output

#include <ADS1220_WE.h>
#include <SPI.h>

#define ADS1220_CS_PIN    7 // chip select pin
#define ADS1220_DRDY_PIN  6 // data ready pin 
#define VREF 2.0 // Reference Voltage, value does not matter

ADS1220_WE ads = ADS1220_WE(ADS1220_CS_PIN, ADS1220_DRDY_PIN);

void setup(){
  Serial.begin(9600);
  if(!ads.init()){
    Serial.println("ADS1220 is not connected!");
    while(1);
  }

  ads.setCompareChannels(ADS1220_MUX_1_0);
  ads.setGain(ADS1220_GAIN_32);
  ads.setVRefSource(ADS1220_VREF_REFP0_REFN0);
  ads.setVRefValue_V(VREF);  // value doesn't matter, the ratio is important
  ads.setIdacCurrent(ADS1220_IDAC_500_MU_A);
  ads.setIdac1Routing(ADS1220_IDAC_AIN1);
  ads.setIdac2Routing(ADS1220_IDAC_AIN0_REFP1);
} // end of setup()

void loop(){
  float result = 0.0;
  float pt100ResistanceInOhm = 0.0; 
  float leadResistanceInOhm = 0.0;
  float temperature = 0.0;
  float ambTemp = 0.0;
  
  ads.enableTemperatureSensor(true);
  ambTemp = ads.getTemperature();
  ads.enableTemperatureSensor(false); 
  Serial.print("Ambient Temperature [°C]: ");
  Serial.println(ambTemp);

  ads.setCompareChannels(ADS1220_MUX_REFPX_REFNX_4);
  result = ads.getVoltage_mV();
  Serial.print("Reference Voltage [mV]:   ");
  Serial.println(result * 4.0);
  
  ads.setCompareChannels(ADS1220_MUX_1_0);
  result = ads.getVoltage_mV(); // get result in millivolts
  pt100ResistanceInOhm = result * 2.0 * 2.403 / VREF; // Reference resistor: 2.403 kOhm
  Serial.print("Resistance PT100 [Ohm]:   ");
  Serial.println(pt100ResistanceInOhm);
 
  temperature = 1.01898*pow(10,-3)*pow(pt100ResistanceInOhm,2) + 2.35443*pt100ResistanceInOhm - 245.633;
  Serial.print("Temperature [°C]:         ");
  Serial.println(temperature);
  
  Serial.println();
  delay(2000);
}

And here is the output:

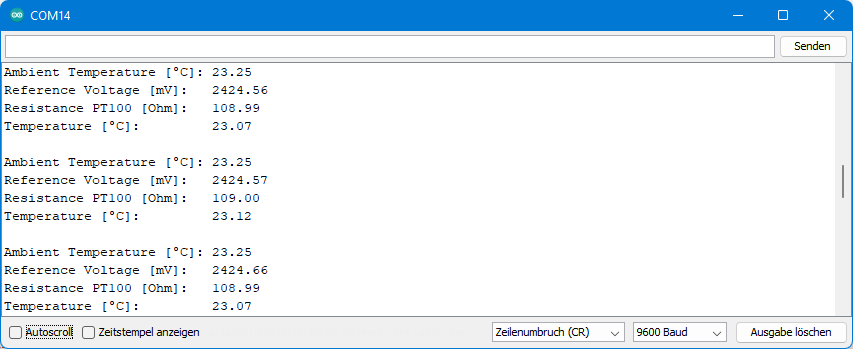
The temperature values determined with the PT100 matched well the measurements of the ADS1220’s internal thermometer (“Ambient Temperature”) and my precise reference thermometer.

Again, the reference voltage is a little bit higher than expected. But as with the previous example, it doesn’t matter as long as the error is IDAC-related. I should mention, however, that although IDAC1 and IDAC2 can deviate from the target by up to 6 percent according to the data sheet, the difference between IDAC1 and IDAC2 is a maximum of 0.3 percent. Only this makes the measurement sufficiently accurate.

And one more note: If you try this example yourself by testing this on a breadboard and connecting the PT100 with alligator clips, be aware that you will create significant unwanted resistance. If your determined PT100 resistance deviates by only one ohm, this results in a temperature deviation of three degrees! The PT1000 is much less sensitive in this respect.

4-wire circuit

4-wire RTDs are even more accurate. The following circuit eliminates the influence of the leads:

The calculation is even simpler because we use only one IDAC.

U_{\text{AIN1-AIN0}} = I_{\text{IDAC}} \cdot R_{\text{PT100}} 

U_{\text{REF}} = I_{\text{IDAC}}\cdot R_{\text{REF}}

R_{\text{PT100}}  =\frac{U_{\text{AIN1-AIN0}}}{U_{\text{REF}}}\cdot R_{\text{REF}}

For example, at 5 volts supply voltage, you could choose a 4.7 kΩ resistor as R_REF and 500 microamps as IDAC. You should now be able to create a sketch for this yourself. Since I had no 4-wire PTC available, I have not tried the circuit.

Wheatstone bridges with the ADS1220

As a final application example, let’s look at Wheatstone bridge circuits. These are used to determine small resistances or small resistance differences, e.g. when using strain gauges. Maybe you have already worked with it without knowing it. Many load cells are based on Wheatstone bridges of strain gauges. But I won’t go into the theory here, because that would take us too far.

The circuit is very simple:

The supply voltage of the bridge is also the reference voltage. The output voltage of the bridge is measured as the difference between two inputs of the ADS1220. The cool thing is that the output voltage is proportional to the input voltage and therefore also to the reference voltage. Fluctuations in the supply voltage therefore do not play a role.

And this is where the Low Side Switch comes into play. If you activate the function, the low side switch closes during a measurement. Otherwise, it is open and thus prevents the bridge from consuming power unnecessarily. 

For testing, I dug out my bending plate with Wheatstone bridge from the post on strain gauges again:

The associated sketch is simple:

#include <ADS1220_WE.h>
#include <SPI.h>

#define ADS1220_CS_PIN    7 // chip select pin
#define ADS1220_DRDY_PIN  6 // data ready pin 

/* Create your ADS1220 object */
ADS1220_WE ads = ADS1220_WE(ADS1220_CS_PIN, ADS1220_DRDY_PIN);

void setup() {
  Serial.begin(9600);
  if (!ads.init()) {
    Serial.println("ADS1220 is not connected!");
    while (1);
  }

  ads.setCompareChannels(ADS1220_MUX_1_2);
  ads.setGain(ADS1220_GAIN_128);
  ads.setVRefSource(ADS1220_VREF_REFP1_REFN1);
  ads.setVRefValue_V(5.0);  // The exact value doesn't matter!
//  ads.setRefp1Refn1AsVefAndCalibrate(); // That will not work here!!
  ads.setLowSidePowerSwitch(ADS1220_SWITCH);  
} 

void loop() {
  float result = 0.0;
  result = ads.getVoltage_mV(); // get result in millivolts
  Serial.print("Bridge Voltage [mV]: ");
  Serial.println(result, 3);
  
  delay(2000);
}

In this case, the gain can be set to 128 because the output voltage of the bridge is only a few millivolts. The PGA does not need to be bypassed as there is no danger of approaching AVDD or AVSS to 200 millivolts.

This is what the output looked like when I pressed down on the bending plate and then let it relax again:

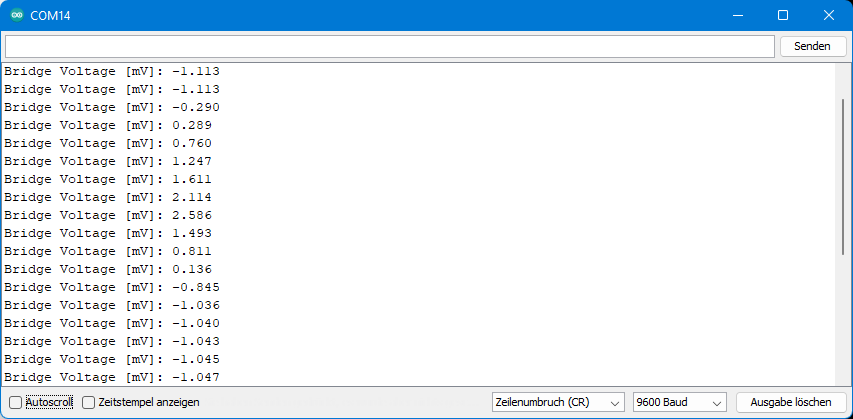
I reduced the bridge voltage from 5 volts to 3.3 volts without changing the sketch. The measured values did not change. Of course, the output voltages are then no longer correct. But they don’t have to, since values stand for certain strains or (weight) forces. And they are supposed to be independent of the bridge voltage fluctuations.

If this bothers or confuses you, then you might as well work with the raw values (via getRawData()) instead of the voltages.